Thermal decomposition of nickel carbonyl

Kipnis A. Ya., Michailova N. F., Pomeranzeva L. A., Rumshin A. E.

Kinetics and mechanism of thermal decomposition of nickel tetracarbonyl

with the formation of nickel aerosols

 

 

 

 

Ni (CO)₄ = Ni (CO)₃ + CO  

 

 

Ni_g(CO)_x + Ni_j(CO)_y → Ni_g+j(CO)_z + (x + y - z)CO  

g, j = 1, 2, 3, ...

 

It is suggested that the activation energy for aggregation would fall from 9 kcal/mole at g + j = 2 to zero at g + j ≥ 13.

 

 

 

 

 

 

 

 

А. Я. Кипнис, Н. Ф. Михайлова, Л. А, Померанцева, А. Е. Рюмшин

 

МЕХАНИЗМ И КИНЕТИКА ТЕРМИЧЕСКОГО РАЗЛОЖЕНИЯ ТЕТРАКАРБОНИЛА НИКЕЛЯ В ОБЪЕМЕ

Статья депонирована в ВИНИТИ в 1979 : № 2714-79;

реферат

опубликован в "Журнале прикладной химии" 1980, 53, №6, с. 1439-1440

 

I. ВВЕДЕНИЕ

Термическое разложение карбонила никеля (КН) в объеме  с получением никелевых порошков имеет существенное прикладное значение. Вместе с тем этот процесс является характерным при­мером "химической кристаллизации" из газовой фазы и с этой точки зрения его исследование представляет более общий тео­ретический и практический интерес.

Несмотря на то, что термическому разложению КН в объеме посвящен ряд исследований [1-7]  (см. табл.1),  сведения о законо­мерностях процесса неполны и противоречивы. Это обусловлено различиями в условиях проведения упомянутых исследований, а также тем, что в большинстве работ наблюдали лишь суммарнуюскорость сложного процесса, причем в условиях, когда все его стадии, в том числе и заключительные, получали значительное развитие.

В настоящей работе излагаются результаты комплексного исследования термического разложения КН в объеме; применены следующие методы: I) измерение кинетики с применением специально разработанных проточных дифференциальных реакторов, обеспечивающих наблюдение результатов процесса при малых временах раз­ложения (от 0,02 до 3 сек); 2) измерение счетной концентрации и размера частиц образующегося аэрозоля никеля; 3) электронно-микроскопическое исследование твердых продуктов разложения; 4) математическое моделирование процесса на ЭЦВМ как средство расшифровки наблюдаемых экспериментально зависимостей.

Ранее по результатам расчета равновесий гомогенной диссоциации КН и существующим литературным данным была намечена общая схема процесса [8]; рассмотрены возможные пути его ма­тематического описания [9] и разработана математическая   мо­дель процесса,  основанная на его микрокинетическом описании [10, 11, 12]. Результаты этих работ использованы для обсуж­дения и анализа экспериментальных данных.

2.  МЕТОДИКА   ИССЛЕДОВАНИЯ

При разработке методики кинетических измерений ставили за­дачу определения за данное время как степени превращения КН, так и числа и размера возникших частиц. Наблюдение ранних стадий развития процесса возможно при выполнении по крайней мере двух условий. Во-первых,  необходимы весьма большие разбавления пара КН: в противном случае образующийся аэрозоль быстро скоагулирует. Во-вторых, время пребывания веществ в реакторе должно быть настолько кратким, чтобы достигнутая за это время степень превращения оставалась невысокой.

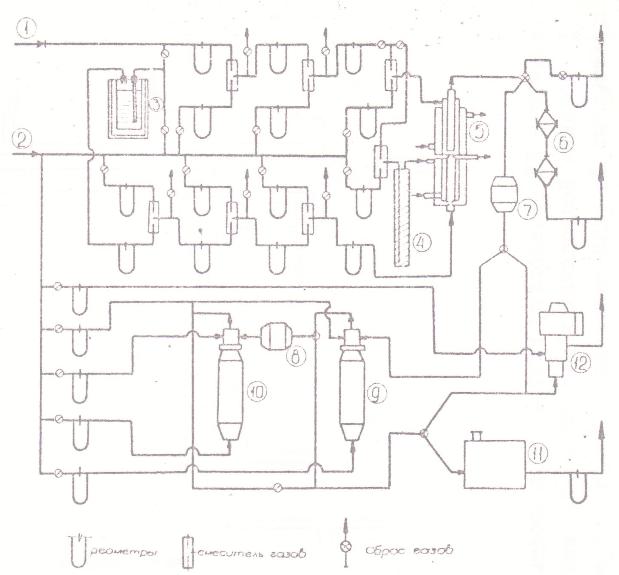
Для того, чтобы удовлетворить этим требованиям, использо­вали  проточные дифференциальные реакторы с малым объемом реакционной камеры, и образующийся аэрозоль никеля исследо­вали в потоке, определяя его весовую и счетную концентрацию. Общая схема установки показана на рис.1; установка включает в себя последовательно размещенные по ходу потока устройст­ва для очистки, нагрева и дозирования газов; реакционный ап­парат; измерительную систему для исследования аэрозоля.

Техника исследования аэрозолей была аналогична описанной в работах  [13-15]. Весовую концентрацию аэрозолей определяли, удавливая частицы никеля фильтрами Петрянова  [16]  с последующим сжиганием фильтра, растворением осадка и колориметрическим определением диметилглиоксимата никеля. При времени накопления осадка на фильтре 10 мин можно было измерять до 10^-10 г Ni в 1 см³.

Степень превращения находили по соотношению между количеством никеля, найденным на фильтре, и количеством никеля, введен­ным в реактор в виде КН.

Для определения счетной концентрации её предварительно снижали пропусканием аэрозоля через одни или два неселективных "разбавителя"  [17], в которых из определенной (большей) части потока аэрозоля отфильтровывались твердые частицы.    Кратность снижения счетной концентрации можно было изменять от 10-20 до3000-5000 раз.

Коммуникации до фильтров и до "разбавителей" стремились сделать идентичными по геометрическим характеристикам, т.е. по сечению, длине и конфигурации.

Чтобы сделать возможным ультрамикроскопическое наблюдение и счет весьма малых частиц, их предварительно "проявляли" (укрупняли) конденсацией на них пересыщенных паров стеарино­вой кислоты, а затем диизобутилфталата в двух последовательно установленных конденсационных укрупнителях типа КУСТ [18]. Для счета частиц применяли прибор системы ЛенНИИ Гигиены тру­да и профзаболеваний, представляющий собой проточный ультрамикроскоп с приспособлением для счета частиц в момент кратковременной остановки потока  [19, 20].  Для определения одного

значения счетной концентрации производили 45-50 отсчетов; при работе вдвоем измерение продолжалось около 1 мин. Для предварительного полуколичественного контроля счетной концентрации аэрозоля использовали нефелометр КОЛ-45 [21], Это позволяло быстро корректировать или изменять режим.

Газы в систему подавали после тщательной очистки от кислорода на активной меди и от пыли на фильтрах Петрянова (узлы  очистки не показаны ка схеме рис. 1); кроме того, оказалась необходимой тщательная подготовка всех коммуникаций. Полноту очистки газов контролировали холостыми измерениями: потоки горячих разбавляющих газов без КН и пар КН без нагрева не пока­зывали фона в нефелометре и счета в ультрамикроскопе.

Парогазовую смесь с низкой концентрацией КН получали путем многократного разбавления насыщенного пара КН азотом или окисью углерода. В качестве насытителя служил термостатированный контейнер для жидкого КН,  снабженный насадкой; последняя предотвращала унос жидкого КН в виде мелких капелек. Температуру насыщения изменяли от 0 до 25°С,  поток газа-носителя,  подаваемого в насытитель,  составлял 20-40 см³/мин. Чтобы общий поток карбонилсодержащего газа, подаваемого в реактор, оставался примерно таким же, перед каждым разбавлением большую часть потока сбрасывали. От одного до трех сбросов и разбав­лений было достаточно, чтобы концентрация КН на входе в реак­тор (перед смешением с горячим азотом)  составляла от 10^-5   до 10^-10 г/см³.

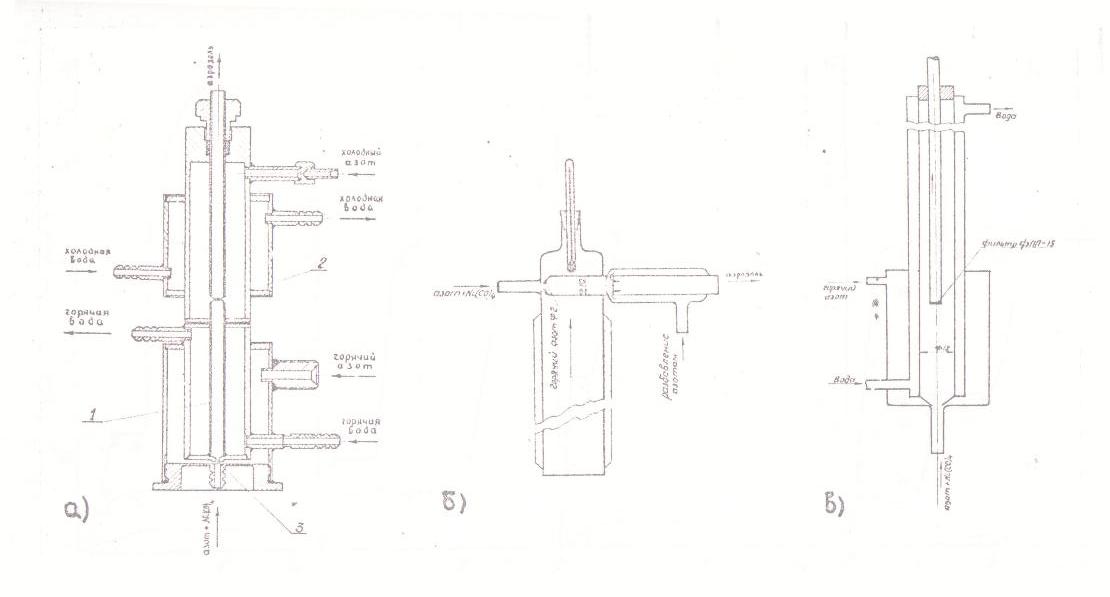
На рис.2 показаны схемы реакторов, использованных для ки­нетических измерений [22]. На входе в реактор малый поток разбавленного пара КН, подаваемый вдоль оси реактора, в щелевом сместитеде пересекается радиально направленным потоком горячего азота, обычно в 20-100 раз превосходящим осевой поток. Время смешения оценивается в 10^-4 - 10^-3   сек. В вариантах реакторов «а» и «б» на выходе из реакционного пространства реакция прерывается за счет смешения с холодным азотом,  и аэрозоль поступает на определение весовой и счетной концентрации.

В варианте «в» аэрозоль полностью улавливается на выходе из реакционной зоны. В этом варианте счетная концентрация не измеряется, но обеспечивается надежное определение степени превращения,  свободное от погрешности за счет осаждения аэрозольных частиц на стенках реактора и коммуникаций. С помощью этого реактора можно было изменять время пребывания парогазо­вой смеси в реакционном объеме при полном постоянстве условий смешения потоков; для этого перемещали вдоль оси реактора от­водящую трубку с фильтром. Диапазон изменения времени контак­та -  от 0,2 до 2,2 сек  -  обеспечивал возможность достижения измеримых степеней превращения при низких температурах.  Можно было опасаться ошибки за счет вклада гетерогенной реакции на фильтре и, тем более, на частицах никеля,  однако,  оценки величины этой ошибки (в предположении, что реакция протекает на частицах как на компактном никеле) показали, что в рабочем диапазоне температур (ниже 90°С) возможная погрешность пренебрежимо мала.

В некоторых измерениях,  направленных на наблюдение более поздних стадий процесса,  использовали также простые стеклянные реакторы без щелевого смесителя (требования к быстроте смешения можно было снизить вследствие большой продолкительности времени пребывания в этих реакторах). В одном из них карбонилсодержащую парогазовую смесь подавали в тройник перпендикулярно к основному потоку горячего азота («тройниковый» реактор с объемом реакционного пространства   38 см³). В другом реакторе (сферическом с объемом 260 cм³) радиальный поток парогазовой смеси пересекался перпендикулярным к нему потоком горячего азота. Эти реакторы использовали в опытах, в которых получали крупные (ультрамикроскопического размера) частицы; для определения их счетной концентрации аэрозоль из реактора направляли непосредственно на проточный ультрамикроскоп. Кроме того, в этих реакторах проводили опыты разложения КН при более высоких концентрациях, что позволяло получать пробы карбонильного никеля в количествах, достаточных  для последующего злектронно-микроскопического исследования.

Электронно-микроскопический метод исследования аэрозольных частиц никеля был использован как дополняющий поточные методы. Это обеспечило независимое и прямое определение раз­мера частиц никеля и дало сведения для суждения о процессе их коагуляции.                                              

Изучали два типа объектов. Для исследования частиц,  обра­зующихся при низких концентрациях,  отбирали пробы из потока аэрозоля на выходе из реакторов. Для этого в соответствии с [23]  в поток вводили приклеенную к охлажденному металлическо­му держателю медную сеточку диаметром 3 мм (такие сеточки служат стандартной основой для дисперсных объектов, на которой последние вводятся в камеру электронного микроскопа). Время выдержки при отборе проб составляло от 1 до 50 сек. Пробы отбирали в двух местах -  на выходе из реактора и на входе в первый из приборов КУСТ. Полученные таким образом объекты непосредственно после опыта исследовали с помощью просвечивающего электронного микроскопа "Тесла" В5-242 с разрешающей способностью не хуже 40А.

Опыт показал, что при отборе проб непосредственно после реактора (даже при очень коротком времени экспозиции) на сеточке накапливается много частиц, которые быстро срастаются в большие агрегаты; спеканию способствует и облучение электронным пучком в процессе наблюдения. Поэтому представление о размерах частиц удалось получить только при отборе проб из потока после разбавителей перед первым из приборов КУСТ. Прав­да, и в этом случае осложнения,  связанные со спеканием частиц в электронном пучке, оставались, так что данных, достаточных для построения распределения частиц по размерам, получить не уда­лось. Все же результаты этих измерений были весьма существен­ны для целей настоящей работы,  так как они дали представление о диапазоне размеров частиц никеля и, что оказалось особенно важным,  о характере их агрегации.

Другой тип объектов - пробы порошкообразного карбонильного никеля, которые собирали на выходе из тройникового и сфериче­ского реакторов.  Эти пробы препарировали по методике, предло­женной М. А. Немойтиным [24]: крупные частицы осаждали из взвеси в спирте, а отмученную мелкую фракцию (около 50 мг), 40-50 мин растирали в пленочном растворе (0,5% парлодиона в амилацетате) и затем каплю такой суспензии наносили на поверхность воды в чашке Петри; при растекании капли взвешенные в суспензии частички никеля разбегались вместе с жидкостью и после испарения растворителя оказывались включенными в пленку-подложку на таком расстоянии друг от друга, что спекание их в электронном пучке было исключено.

Измерения, проведенные на этих объектах, дали дополнительные и достаточно надежные сведения о размерах и характере агрегации частиц никеля при разложении КН в объеме.

Параллельно с кинетическими измерениями проводили исследование процесса методом математического моделирования (подробнее см. 4).

Опыт работы и результаты расчетов показали, что ни в одном из вариантов проведения реакции не удается освободиться от или иных осложнений или ограничений. При быстром смешении и малом времени контакта, когда велико отношение поверхности реактора к объему и растет погрешность за счет осаждения частиц на стенках, уменьшение этой погрешности сопряжено либо с замедлением смешения (этот путь был проверен в опытах с тройниковыми реакторами), либо с отказом от измерения концентрации частиц (реактор по схеме рис.2в). Тем не менее, ра­бота с применением всех этих реакторов и с привлечением ос­тальных методов позволила получить достаточно полное пред­ставление о закономерностях протекания процесса.

 

3.  ЭКСПЕРИМЕНТАЛЬНЫЕ    ДАННЫЕ

 

На разных реакторах и в различных режимах было проведено свыше 400 опытов; в табл. 2 приведены типичные примеры серий измерений, показывающие значения параметров экспериментов и измеряемых характеристик процесса.

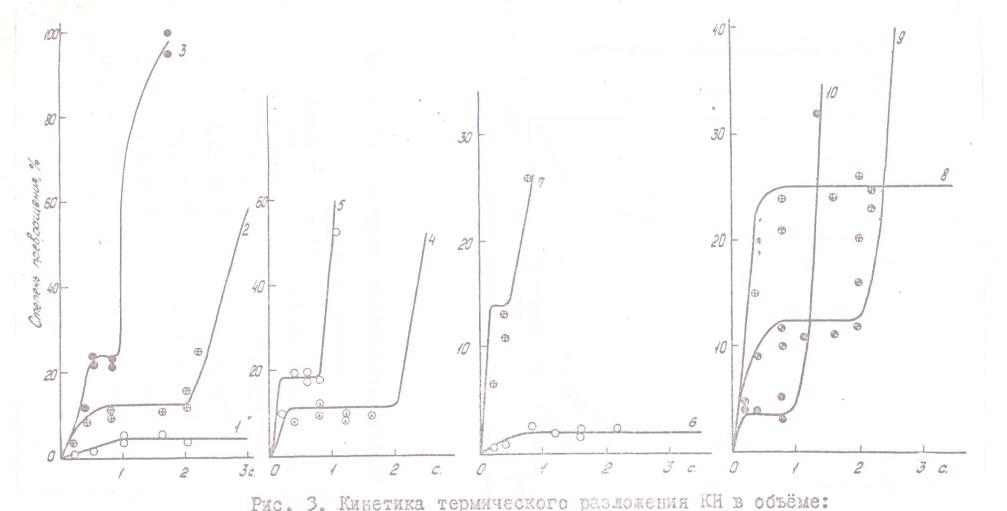
При рассмотрении данных о зависимости степени превращения от условий обращают на себя внимание две особенности. Первая заключается в существовании квазиравновесного этапа развития реакции, который особенно отчетливо проявляется при низких температурах; в некоторых случаях за время наблюдения (до 2 сек) система даже не успевает выйти из этого квазиравновесного состояния (см. рис. 3). Эта особенность реакции ранее, по-видимому, не наблюдалась, что объясняется трудностью ее обна­ружения при использовании статических реакторов со временем установления начальных условий свыше 1 сек.

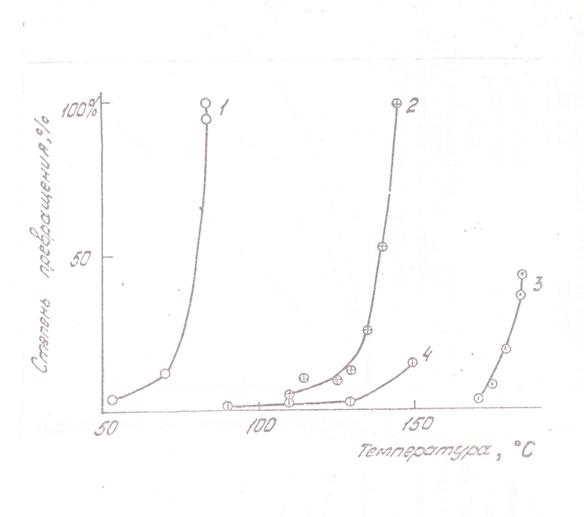
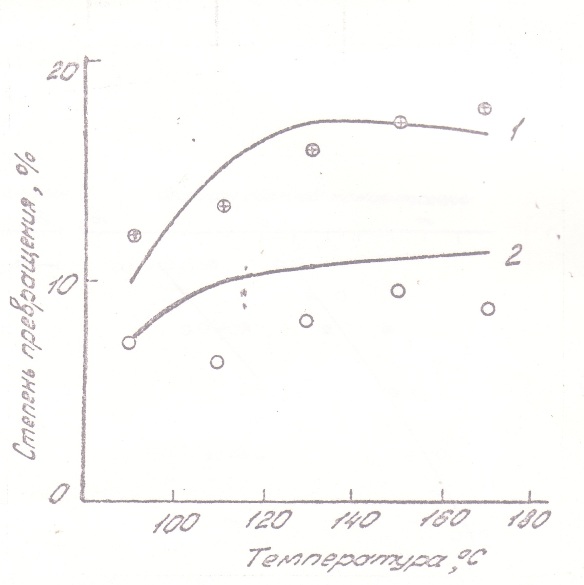
Вторая особенность процесса противоположна первой: за площадкой квазиравновесия реакция развивается лавинообразно, особенно в области более высоких температур и концентраций, поэтому температурная зависимость степени превращения за дан­ное время может быть очень крутой (рис. 4).

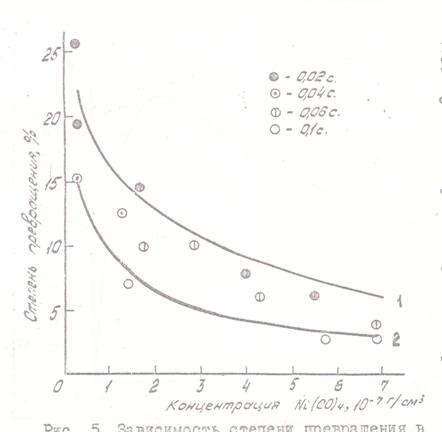
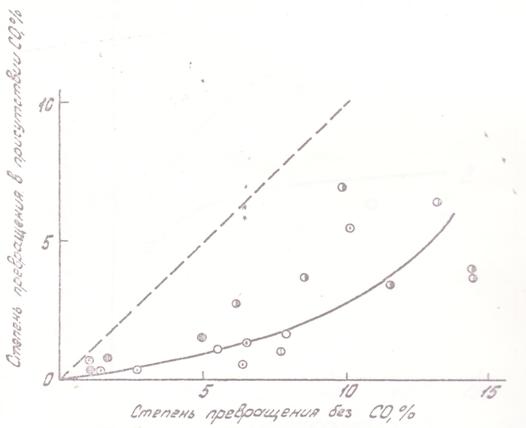
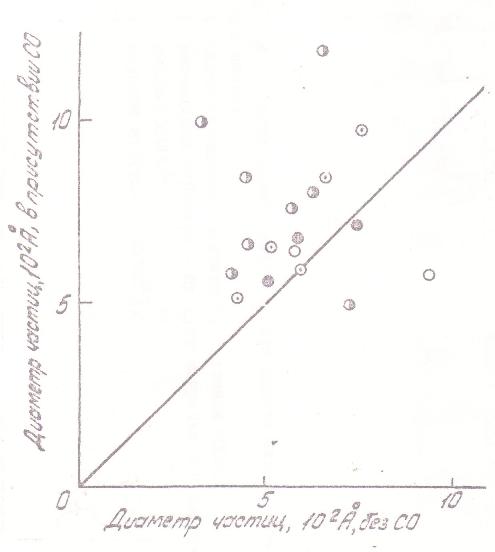
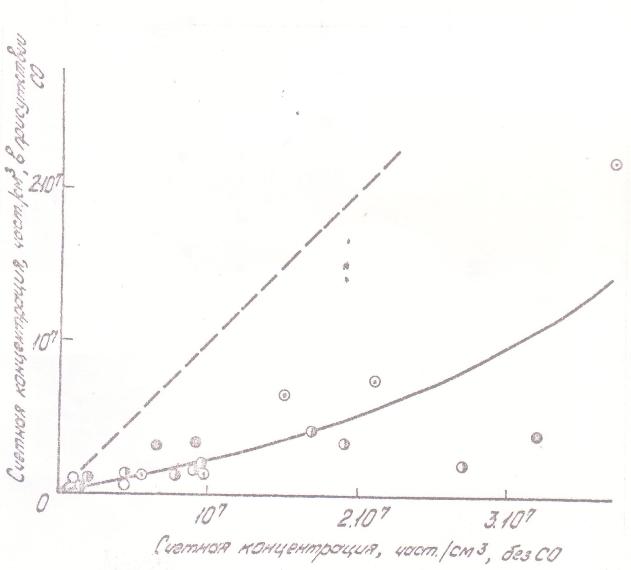
Зависимость степени превращения за данное время от кон­центрации КН выражена более слабо; при этом вследствие торможения продуктом увеличение концентрации КН вызывает снижение наблюдаемой степени превращения (рис. 5). Торможение продуктом было специально прослежено в опытах с введением в газ избытка СО; результаты показаны на рис. 6.

Снижение степени превращения под влиянием окиси углерода является естественным. В области низких температур, как вид­но из рис. 3, удается наблюдать изменение положения квазиравновесия (в сторону меньших степеней превращения) и увеличение продолжительности периода квазиравновесия. Это указывает на то, что присутствие продукта влияет прежде всего на гомо­генную диссоциацию КН.

Приведенные выше данные относятся к условиям практического отсутствия влияния стенок. Они и были использованы при выборе параметров математической модели (см. ниже 4). Измерения   в реакторах типа «а» и «б» (рис. 2)  сопряжены с частичным осаждением аэрозоля на стенках, а при более высоких температурах - также и с заметной гетерогенной реакцией на стенках.

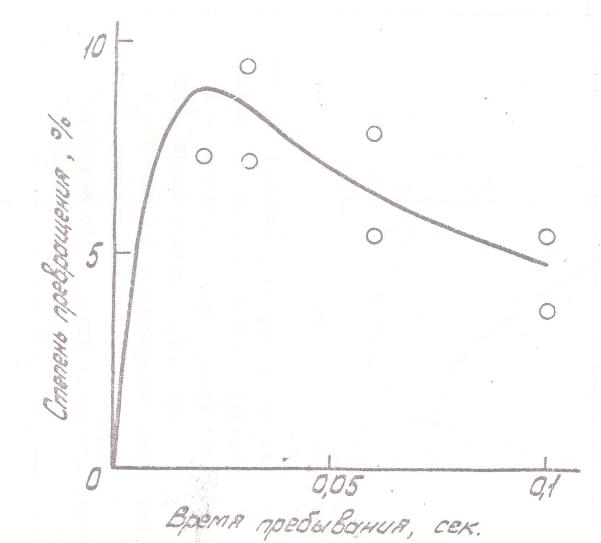
Подробный анализ конкуренции процессов в объеме и на стен­ке требует получения дополнительных данных и не входят в задачу настоящей работы. Заметим, однако, что вклад стенок может составлять около половины наблюдаемой степени разложения, что влияет и на протекание процесса в объеме. Поэтому в математическое описание процесса были введены члены для учета осаждения аэрозольных частиц и гетерогенной реакции на стен­ке. Это обеспечило удовлетворительное согласие опыта и расчета и для условий, где роль стенок была существенной.   На рис.7 и 8 сопоставлены измеренные и рассчитанные степени превращения в объеме, причем расчет выполнен с учетом потерь на стенках реактора. Как видно из этих рисунков, и временная (при t  = const) и температурная (при Т = const) зависимос­ти степени превращения передаются моделью вполне удовлетворительно.

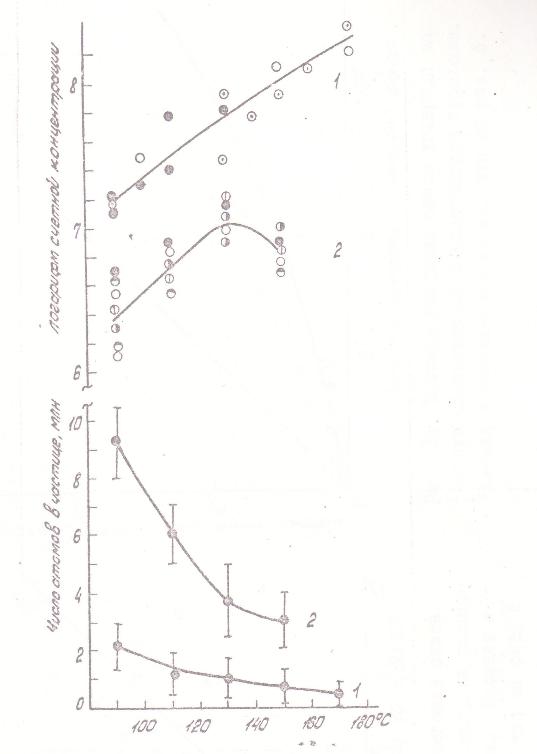
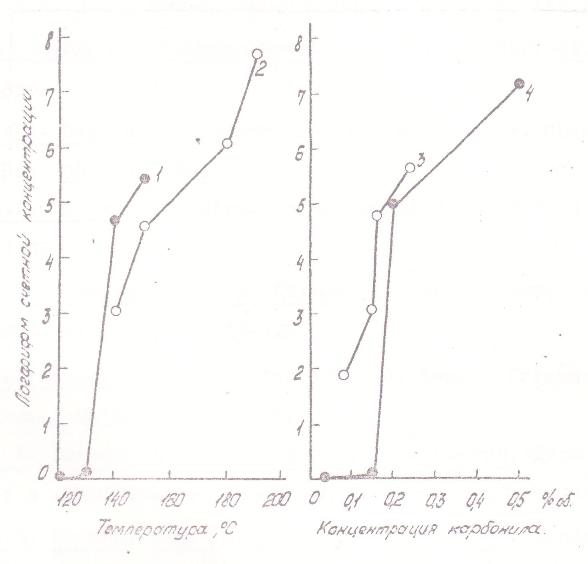
Другая часть полученных данных характеризует процессы роста частиц твердого никеля в зависимости от условий. На рис. 9 представлено изменение счетной концентрации и среднего размера частпц с увеличением концентрации карбонила и с ростом температуры, а на рис. 10 и 11 -  уменьшение счетной концентрации и увеличение среднего размера частиц в присутствии СО. Эти зависимости слабее подвержены влиянию стенок и проявляются достаточно отчетливо. Качественно наблюдаемая картина отвечает представлениям теория конденсации: бóльшим  «химическим пересыщениям»,  т.е. более высоким концентрациям карбонила и температурам отвечает меньший размер и бóльшая концентрация частиц. Смена этих зависимостей на противоположные при больших временах контакта должна быть приписана влиянию коагуляции, опережающей возникновение новых частиц аэрозоля.

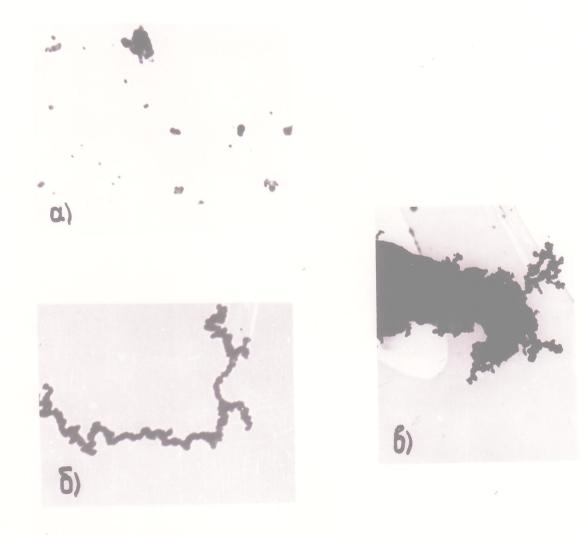
Коагуляционный рост частиц в изучаемом процессе, как выяснилось в ходе исследования, характеризуется необычными особенностями. На рис. 12 представлены электронно-микроскопические фотографии частиц никеля,  свидетельствующие об образовании нитевидных агрегатов сферически частиц. Отсюда следуег, что начиная с некоторого размера частиц никеля их коагуляция становится направленной.  (Впервые это было отмечено в работе  [25]).

Механизм явления установлен Н.А.Фуксом:  он заключается в сближении частиц под действием диффузии на такое расстояние, на котором силы притяжения «достигают заметной величины, после чего движение частиц приобретает упорядоченный характер» [26,  стр. 282,  284]. В результате коагуляция протекает самоускоренно, и процесс роста частиц приобретает   лавинообразный характер. Это явление было прослежено в опытах со сферическим реактором, из которого аэрозоль направляли непосредственно в ультрамикроскоп. При этом наблюдали именно более поздние стадии,  относящиеся к направленной коагуляции. Полученные результаты (рис. 13) подтверждают заключение об ускоренном   протекании коагуляции на этой стадии.

В табл. 3 приведены результаты определения размеров аэрозольных частиц электронно-микроскопическим методом. Эти размеры несколько ниже средних размеров, найденных по весовой и счетной концентрациям аэрозолей, возникших в аналогичных условиях. Следует,  однако, иметь в виду, что числа  табл. 3 относятся только к сферическим частицам, образование которых доказывается электронно-микроскопическими снимками. Поэтому данные двух методов не противоречат, а взаимно дополняют друг друга. Совокупность полученных экспериментальных данных была использована при математическом моделировании процесса.

 

4.   МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА

ТЕРМИЧЕСКОГО РАЗЛОЖЕНИЯ КАРБОНИЛА НИКЕЛЯ В ОБЪЕМЕ

 

В случае столь сложных объектов как рассматриваемый, математическое моделирование становится необходимым методом исследования, без применения которого анализ экспериментальных данных оказывается затруднительным, если вообще возможным.

Как упомянуто, ряд экспериментальных данных качественно согласуетоя с предсказаниями классической теории конденсации. Однако детальный анализ показал [9], что в действительности основная посылка классической теории - о существовании цепочки квазиравновесий между мономерами, докритическими и критическими частицами - не выполняется в большинстве случаев химической кристаллизации.

Применительно к рассматриваемому случаю для узкой области условий, где эта посылка могла бы быть выполнена, были проведены и машинные расчеты, которые подтвердили непригодность классического описания и необходимость микрокинетического подхода к процессу. 

Математическая модель процессов химической кристаллизации в объеме,  основанная на таком подходе, построена и подробно обсуждена в отдельной работе  [12]. Записанная применительно к рассматриваемому случаю, модель учитывает гомогенную диссоциацию КН до одноядерных субкарбонильных осколков, агрегацию этих осколков в многоядерные субкарбонильные комплексы и, далее,  в крупные частицы никеля (т.е. коагуляцию аэрозоля), а также обратимое гетерогенное разложение КН на частицах никеля.

 Использование зтой модели предполагает знание характеристик этих стадий процесса. Кроме того,  как упоминалось, необходим учет осаждения частиц и разложения КН на стенках. В машинных  экспериментах варьировали параметры модели, подбирая их таким образом, чтобы достичь согласия между результатами расчетов и кинетических измерений. Ниже подробно рассматривается эта сторона работы.

Гомогенная диссоциация КН:

Ni (CO)₄ = Ni (CO)₃ + CO                                            (I)

 

Cкорость гомогенной диссоциации КН представлена разностью скоростей прямой реакции (разложение КН) и обратной реакции (синтез КН):

 

V_v = K₁n_k - K₂n₁n_c                                      (1)

 

Здесь n_k , n_c и n₁ - концентрации КН, СО и трикарбонила соответственно.

 K₁ - константа скорости прямой реакции, в соответствии с данными [27] о кинетике изотопного обмена КН с меченой СО, имеет величину

 

K₁  = 3,3·10¹⁴·ехр (-22100/RТ)  сек^-1 ,

 

а константа скорости обратной реакции:

 

К₂ = К₁/К   = 4,1·10⁵Т л/моль·сек.

 

(Константа равновесия (1) К была определена ранее [8]).

(В предварительных машинных экспериментах испытывали также несколько других форм кинетического уравнения и его параметров, в том числе формулу вида

 

V_v = K₁n_k/ (1 + K*n_c )                    (2)

 

со значениями констант по данным различных авторов (см. табл. 1), а также принимали двухступенчатую диссоциацию тетракарбонила до дикарбонила с константами скорости второй ступени в прямом и обратном направлении соответственно  

10¹⁴ · ехр (-30000/RT) сек^-1 и 1,6.10⁷ л/(моль·сек).

Ни в одном из вариантов, кроме основного, указанного вначале, не было получено результатов,  сколько-нибудь приближающихся к экспериментальным данным).

 

Агрегация субкарбонилов:

 

Ni_g(CO)_x + Ni_j(CO)_y → Ni_g+j(CO)_z + (x + y - z)CO   (II)

g, j = 1, 2, 3, ...

 

Здесь z(g+j) - вероятное число групп CO в частице, содержащей (g+j) атомов никеля.

Эта стадия процесса экспериментально не исследована и един­ственное утверждение, вытекающее из опытных данных (масс-спектрометрия [28]),  состоит в том, что такая стадия существует. Поэтому описание кинетики агрегации возможно только на основе более или менее правдоподобных предположений.

Исследованию в машинных экспериментах было подвергнуто три общих предположения, каждое из которых представлялось доста­точно вероятным.

Согласно первому предположению агрегация является незатруд­ненной,  т.е. не отличается от коагуляции (см. ниже). В пользу такого предположения можно выдвинуть следующие доводы. Реак­ция агрегации по характеру близка к реакциям рекомбинации ра­дикалов и потому должна быть незатрудненной. Правда, исследования по конденсации паров выявили весьма низкую эффектив­ность столкновений при образовании кластеров из 2-5 мономер­ных частиц [29]; это связано с трудностью отвода избыточной энергии, необходимого для стабилизации агрегата (стабилизация достигается тем легче, чем сложнее возникающая частица, так как тем вероятнее перераспределение энергии по внутренним степеням свободы). В нашем случае нет необходимости в стаби­лизации за счет тройных соударений, так как имеется другой канал для отвода избыточной энергии -  отщепление карбонильной группы СО от возникшего агрегата. Поэтому предположение о незатрудненной агрегации априори представлялось вполне разумным.

Машинные эксперименты показали, однако, что при этом пред­положении невозможно передать наблюдаемый на опыте "индукцион­ный" (квазиравновесный) период процесса, а время, необходимое для достижения экспериментальных степеней превращения, на по­рядок и даже на два меньше фактического. Поэтому гипотеза о незатрудненной агрегации была отвергнута.

Согласно второму предположению агрегацию рассматривали как затрудненный процесс с эффективностью соударений ß, расту­щей от малой величины ß₂ для реакции между мономерными частицами до 1 для реакции образования агрегата из n* атомов; закон роста   ß   задавали в виде

log ß = log ß₂(n* - g - j)/(n* -2)                  (3)

 

Таким образом,  стадию агрегации характеризовали двумя параметрами: эффективностью столкновения мономерных частиц  ß₂  и шириной диапазона размеров частиц  n*, в котором происходит переход от затрудненной агрегации к обычной коагуляции.

В этом случае оказалось возможным подобрать параметры аг­регации, при которых качественно воспроизводится индукционный период процесса и рассчитанные общие скорости процесса близки к измеренным. Однако температурный ход скорости процесса при различных начальных концентрациях КН передать не удалось. Поэтому и вторая гипотеза о кинетике агрегации была отведена.

Наиболее удачным оказалось третье предположение о термиче­ски активируемой агрегации. Это предположение представляется более обоснованным и из общих соображений: агрегация двух суб­карбонильных осколков есть по существу химическая реакция, и она требует активации, достаточной для удаления избыточных групп СО, препятствующих формированию связи металл-металл; с ростом размера агрегатов удаление СО облегчается и постепенно активационный барьер исчезает - агрегация переходит в обычную коагуляцию.

В уравнении для скорости агрегации

 

V^a = K^a_g j C_Nig(CO)x C_Nij(CO)y                           (4)

 

(символами С обозначены концентрации агрегатов) константа скорости реакции K^a_g, j между частицами из g и j атомов никеля в соответствии с последней гипотезой имеет вид

 

K^a_{g, j} = K⁰_g,j exp [-E(g+j)/RT]                    (5)

 

Для определения предэкспоненциального множителя  K⁰_g,j были проведены расчеты по уравнениям теории соударений и теории абсолютных скоростей реакций. Энтропию активированного ком­плекса при этом принимали равной энтропии агрегата  Ni_g+j(CO)_x+y .   Анализ показал, что стерический множитель равен единице. Величина   K⁰_g,j ,  таким образом, может рассматриваться как коэффициент газокинетической коагуляции (см.ниже). Энергия активации реакции агрегации равна

 

E (g + j)  = E^a · (n* - g ? j)/(n* - 2)         (5)

n*³ g+ j ³2

Принятое линейное падение энергии активации с размером обра­зующейся частицы является простейшим правдоподобным допуще­нием.  При значениях   g + j  >  n* величина Е(g +j)  принимается равной нулю и агрегация считается незатрудненной.

Таким образом, термически активируемую агрегацию характери­зовали двумя параметрами, вполне аналогичными параметрам пре­дыдущей гипотезы: энергией активации реакции между мономерными частицами Е^а и шириной интервала размеров n*, в которой ак­тивированная агрегация постепенно становится неактивированной. Значения этих параметровварьировали в следующих диапазонах:

E^o  -  от 3 до 22 ккал: первое число отвечает нижнему пре­делу  теплового эффекта реакции

Ni(CO)₃ = Ni₂(CO)₅ + CO                         (III)

 

а второе -  прочности связи Ni-СО в Ni₂(CO)₆;

n*  -    от 3 до 12 (нижнее значение отвечает активированной агрегации только мономеров, верхнее -  всех частиц, для которых реакция вида    (III),   т.е.  с отщеплением одной карбонильной группы, может быть эндотермичной.

По результатам машинных экспериментов была выбрана следующая наилучшая комбинация:

 

Е^а  = 9 ккал,       n*  =12.

Принятое значение E^o  отвечает верхнему пределу теплового эффекта реакции (III).

Разумеется,  описание кинетики агрегации, на котором мы ос­тановились, нельзя считать доказанным, но оно, с одной сторо­ны, является физически осмысленным, а с другой -  не противоре­чит имеющимся экспериментальным данным.

Коагуляция

По мере роста частиц их агрегация перестает быть затрудненной и может рассматриваться как обычная газоки­нетическая коагуляция. Константа скорости такого процесса, или «коэффициент коагуляции» [30], в предположении о сферичности частиц и об их слиянии при столкновении, выражается известным соотношением кинетической теории газов:

 

K_gj  = π (r_g + r_j)2 [(8kT/π).(m_g + m_j) / m_gm_j]^1/2                     (7)

 

где  r_g  и  r_j - радиусы частиц, а m_g + m_j - их массы. В случае однокомпонентных частиц это соотношение переходит в более простое [31]:

 

K_gj  = (9 π/16 ρ_Ni)^1/3 m₁^1/6(kT)^1/2 (g^1/3 j^1/3)2[(g+j)/gj]^1/2     (8)

 

Здесь m₁ - масса первичной частицы (атома никеля) а  ρ_Ni - плотность частиц, предполагаемая не зависящей от их размера.

В случае частиц  Ni_g(CO)_x и Ni_j(CO)_y  такое упрощение, особенно при небольших g и j, вызывает завышение вычисляемой величины K_gj. Легко, однако убелиться, что эта ошибка незначительна: так для частиц, содержащих 100 атомов никеля (состав  Ni₁₀₀(CO)₆₃, см. ниже), K_gj  завышается на 10% и даже при g=10  ошибка не превосходит 25%.

С другой стороны, поправка к значению  K_gj, учитывающая влияние молекулярных сил на эффективное сечение столкновений, представляет собой множитель, равный 2-3 [1З, 30]. Исходя из этих, соображений величину коэффициента коагуляции приняли рав­ной   2 K_gj , где  K_gj  задана формулой (8). Этот выбор пред­ставляется логичным и первоначально в расчетах использовали именно такие величины коэффициентов коагуляции.

Однако результаты предварительных вычислений показали, что на опыте наблюдаются гораздо большие размеры частиц, чем дает расчет, а счетная концентрация на несколько порядков ниже вы­численной. Это расхождение заставило обратить внимание на то, что формула (8) пригодна лишь для таких частиц никеля, магнит­ное взаимодействие между которыми пренебрежимо мало.

Расчет множителя   ß^M , на который увеличивается газокинети­ческая константа коагуляции вследствие диполь-дипольного вза­имодействия между частицами, выполнен в работе Цебеля [32]; окончательный результат имеет вид

 

ß^M = 1/R_o² (m_g m_j /kT)^2/3                          (9)

 

где R_o - сумма газокинетических радиусов,  а m_g   и  m_j  -дипольные моменты частиц. Для ферромагнитного никеля m_g  =  0,604 Ω m_B  g, где  m_B - магнетон Бора, 0,927.10^-20 эрг/эрст,  а   Ω -  отношение намагниченности насыщения при температурах Т°К и 0°К.

Учитывая, что для простейшего случая одинаковых g-атомных частиц (1/2). R_o  = 1.41.10^-8.g^1/3 см, находим, что при Т = 600°К   ß^M  = 2,3.10^-4.g ^2/3 . Отсюда, положив  ß^M = 1, по­лучаем минимальный размер частиц, g_o , начиная с которого коагуляция становится направленной:  g_o = 3.10⁵ . Легко убедиться, что в случае неодинаковых частиц условие  ß^M  > Iможет быть выполнено лишь, если наименьшая из частиц имеет размер  g ³ g_o .

Результаты этих оценок были сопоставлены с данными элек­тронно-микроскопических исследований нитевидных агрегатов ма­лых частиц никеля. Измерения минимальных диаметров частиц в таких агрегатах, возникших при 600 °К (выполненные на фотоснимках с общим увеличением 50-60 тыс.), показали, что агрегация становится направленной при диаметре частиц 230-240 Å ,  т.е. g> 5.10⁵ атомов. Это хорошо согласуется с приведенными выше результатами расчета по уравнению (9), особенно если учесть, что расчетное значение  g_o = 3.10⁵ есть нижняя граница, начиная с которой фактор ß^M  становится больше 1. Подставляя экспериментальную величину g= 5.10⁵ в (9), получаем разумный результат ß^M  = 6,2. Для частиц, возникших при 150^оС (423^оК) опыт дал g > 1,5.10⁵, откуда ß^M  = 2.

Таким образом, для учета магнитных взаимодействий при коагуляции можно использовать соотношение (9). После подста­новки в (9) значений входящих в него параметров, в том числе температурной зависимости намагниченности насыщения никеля, получаем простую расчетную формулу

ß^M  = (688 - T).10^-5. (gj)^2/3/ (g^1/3+j^1/3)²                                    (10)

 

Разумеется, следует отдавать себе отчет в том, что при уче­те магнитных взаимодействий описание коагуляции остается при­ближенным, поскольку крупные частицы не успевают сливаться между соударениями и приобретают вытянутую форму; в результате газокинетическая формула становится неточной. Тем не менее, именно введение фактора ß^M  позволило устранить возникшее вначале резкое расхождение расчета и эксперимента.

 

Осаждение частиц на стенках реактора

учитывали введением добавочного члена во всех уравнениях для изменения концентра­ций частиц. Ввиду турбулентного характера движения потока в реакторе скорость осаждения выражали соотношением [23,  стр.240] :   

 

J = αD^3/4n_gRe^7/8n ^1/4/57r      част/см²·сек                               (11)

 

Здесь D - коэффициент диффузии g-атомных частиц; n_g - их концентрация в объеме; r  - радиус канала; n - кинематическая вязкость газа; α - множитель порядка единицы. Учитывая, что критерий Рейнольдса  Re = 2wr/n  (w - линейная скорость потока), и выражая D и  n подходящими интерполяционными формулами, получили расчетное соотношение, в котором поток на стенку отнесен к единице объема реактора (цилиндрического):

 

V^oc_g = w^7/8 n_g /T ^7/16 r ^9/8 g ^3/8     част/сек.см³            (12)

 

Гетерогенная реакция на частицах и на стенках.

Кинетика ге­терогенной реакции на поверхности компактного никеля опреде­ляется     уравнением

 

V_∞ = K₃p_k(10^-6 + p_k) · (1 - p_c⁴/K_pp_k)/(0,01+K₄p_c+K₅p_k)²           (13)

 

Уравнение (13) уточнено по сравнению с ранее опубликованным [34] для очень малых содержаний КН в газе. Индекс ∞ указывает на то, что значение скорости относится к компактномуникелю;   р_k  и р_c  обозначают парциальное давление КН и СО соответственно; второй сомножитель в числителе учитывает обратимость реакции, значения кинетических констант равны:

K₃ = 4,32.10¹³ exp (-22300/RT) г/см².мин.атм²;

К₄ = 8,21.10^-4 ехр( 10300/RТ)    атм^-1;

К_о - 7,70.10⁴ ехр(- 5000/RT)    атм^-1;

K_p - константа равновесия - равна К_p   = ехр(100,2Т - 34000)/RТ).

Способ учета изменения скорости при переходе от плоской по­верхности никеля к малым (g -атомным) частицам,  обладающим избыточной энергией U_g, рассмотрен ранее [9, 34]:

 

V_g =V_пр exp(-U_g/2RT) - V_обр exp (U_g/2RT)              (14)

 

Здесь V_пр и V_обр обозначают скорости прямой и обратной гетерогенной реакции на компактном никеле.

Аналогично записывается скорость гетерогенной реакции на стенке: по экспериментальным данным [34]

 

V_ст = V_∞ exp [-60000/(n + 12)RT]                                (15)

 

Здесь n - число атомных слоев никеля на стенке.

 

Характеристика частиц.

В процессе участвуют разнообразные частицы общей формулы

Ni_g(CO)_x , при малых g представляющие собой субкарбонильные комплексы, а при больших g - частицы никеля с хемосорбированной на их поверхности окисью углерода. В принятом приближении x - число групп СО - определяется только числом атомов никеля в частице g и не имеет самостоятельного значения. Однако знание количества связанной с никелем окиси углерода необходимо для определения, из условия материального баланса, концентрации СО в газовой фазе. Исходя из термодинамических характеристик частиц [35, 36] и из геометрических соображений была принята следующая зависимость числа групп СО в частице от g:

 

z(g) = 1,11 + 1,89g   при  g < 10

z(g) = 14,35 + 0,565g  при   75 > g ³ 10             (16)

z(g) = g_s   при  g ³ 75

Здесь g_s  есть число поверхностных атомов в кластере Ni_g.

 

Для определения  g_s  в функции от общего числа атомов g в кластере из металлических шариков строили модели сферической формы с неупорядоченной упаковкой (для этого шарики покрывали липким составом) с числом шариков в модели от 14 до 100. Хотя результаты этих опытов показали некоторую немонотонность зависимости g_s от g, для целей настоящей работы можно было удовлетвориться следующей аппроксимацией:

 

g_s  =  g [1 - 0,0033(g -1)]                 при  g < 75

g_s  =  3,2g^2/3                      при  g ³ 75               (17)

 

Через число поверхностных атомов  выражали и поверхность частиц, предоставляемую для гетерогенной реакции; она равна 0,78.10^-15 g_s см²; числовой множитель отвечает площади, приходящейся на один поверхностный атом никеля.

Избыточная энергия кластеров  Ni_g  (на 1 грамм-атом никеля), входящая в уравнение (14), дается простой формулой [36]

 

U_g = 85000g^-1/3  ккал/г-атом                       (18)

 

Наконец, коэффициент диффузии частиц, необходимый для определения скорости их осаждения на стенках аппаратуры, представили простой интерполяционной формулой

 

D_g = (0,793/g^1/2).(T/293)^3/2  см²/сек            (19),

 

которая построена по значениям, предложенным Н. А. Фуксом [37]. Для g=1 использовали значение 0,07 см²/сек (коэффициент диффузии карбонила никеля в СО при 20^о).

Пригодность построенной математической модели и выбранных значений ее параметров иллюстрируется приведенными выше рисунками, в особенности данными рис. 3.

Хотя полного совпадения расчетных и измеренных величин протяженности и высоты площадок квазиравновесия добиться не удалось, учитывая с одной стороны сложность и неустойчивость процесса и с другой - неизбежные погрешности измерений и вычислений, следует признать, что согласие между результатами эксперимениального исследования процесса и его математическим описанием является вполне удовлетворительным. Достаточно хорошо модель учитывает и осложнения, связанные с влиянием стенок (рис. 5, 7, 8).

 

5. ОБСУЖДЕНИЕ  РЕЗУЛЬТАТОВ

Последний из опубликованных обзоров, посвященных кинети­ке разложения карбонила никеля заканчивается выводом: «не найдено логической последовательности стадий, которая давала бы наблюдаемый суммарный процесс» [38]. Действительно,  тради­ционное кинетическое описание процесса химической кристалли­зации в объеме оказывается невозможным: оно недостаточно для учета практически бесконечного числа стадий,  слагающих такие процессы.

Результаты измерений и расчетов показывают, что для суммарного процесса разложения КН в объеме определение обычных кинетических характеристик -  энергии активации и порядков реакции -  лишено смысла, т.к. даже сравнение скоростей про­цесса при равных степенях превращения (что является наиболее строгим) в зависимости от выбранного диапазона условий дает различные значения кинетических характеристик; это обуслов­лено изменениями соотношения вкладов разных стадий при изме­нении условий. В частности, наблюдаемая энергия активации процесса может принимать значения от 5 до 60 ккал/моль.    С этим, очевидно, и связаны резкие расхождения в результатах различных авторов.

С другой стороны, полученные данные несовместимы и с рас­пространенным представлением об образовании частиц металли­ческого никеля в результате физической конденсации атомного пара никеля, который первоначально возникает за счет полного разложения КН.

Более того, оказалось, что протекание процесса не может быть описано и с помощью представлений классической теории конденсации, модифицированной применительно к обратимым хи­мическим реакциям [9]. Даже когда качественная картина сог­ласуется с этими представлениями, как, например, в случае введения в газ окиси углерода, механизм наблюдаемых изменений заключается не в увеличении размера критических зароды­шей при снижении пересыщения, а в действии кинетических фак­торов. Именно увеличение среднего размера частиц в присутст­вии окиси углерода являются естественным следствием торможе­ния продуктом начальных стадий разложения: замедление обра­зования субкарбонильных осколков в конце концов приводит к тому, что и коагуляция малых частиц и гетерогенное разложе­ние остающегося  КН происходят на сравнительно неболь­шом числе первоначально возникших крупных частиц. Такой ход процесса наглядно прослеживается в машинных экспериментах [12].

Удовлетворительное описание химической кристаллизации ни­келя при термическом разложении КН достигнуто на основе мик­рокинетического подхода, который учитывает следующие стадии процесса:

(I) гомогенную диссоциацию Ni(CO)₄ до Ni(CO)₃ + CO;

(II) активированную агрегацию субкарбонильных осколков с образованием первичных частиц никеля:

(III) коагуляцию аэрозоля никеля;

(IV) гетерогенное разложение карбонила на частицах никеля со скоростью, зависящей от их размера.

Основания для выбора значений параметров отдельных стадий, установленных в настоящей работе, приведены выше. Хотя нельзя исключать возможности описания процесса и другим набором пара­метров (в особенности это относится к кинетике агрегации, для которой прямые измерения отсутствуют), все же принятые значе­ния кинетических параметров стадий представляются весьма вероятными.

Дальнейшее исследование рассматриваемого процесса (и подоб­ных ему процессов химической кристаллизации в объеме) требует специальных прямых измерений свойств и реакций кластеров, в нашем случае -  многоядерных субкарбонилов никеля.

Последний вопрос, на котором необходимо остановиться,  отно­сится к возможности использования результатов настоящего ис­следования в технологии производства дисперсного карбонильно­го никеля.

Прежде всего, полученные экспериментальные данные непосред­ственно указывают условия получения никеля в наиболее высокодисперсном состоянии,  которое доступно для карбонильных метал­лов. Как явствует из чисел табл.2 (п.п. 40 и след.), применяя описанную в работе технику генерации и закалки высокодисперсных частиц, возможно получить никель дисперсностью в 10-15Å .

Улавливая эти частицы органическими жидкостями, получали фер­ромагнитные суспензии для коллоидно-химических исследований, могущие найти и прикладные применения.

Далее, полученные данные позволили выяснить основные эта­пы формирования частиц карбонильных никелевых порошков; в ус­ловиях технологического процесса эти этапы протекают столь быстро, что наблюдению не поддаются. Отсюда, в свою очередь, вытекают некоторые следствия относительно способов воздейст­вия на технологический процесс.

Именно, переход к промышленному аппарату требует учета преж­де всего двух осложнений -  замедленности смешения поступающе­го пара с горячим содержимым аппарата и присутствие в газе с самого начала разложения свежей порции карбонила, ранее возник­ших частиц никеля. Исследование этих вопросов на основе разработанной математической модели и установленных выше ее пара­метров -  предмет самостоятельной работы; однако качественные выводы о возможности регулирования процесса изменением условий смешения и циркуляции газовзвеси в аппарате очевидны непосред­ственно.

Весьма важным технологическим показателем является "качест­во" порошка карбонильного никеля, характеризуемое его насыпным весом и определяемое характером агрегации первичных частиц ни­келя.

Выше было видно, что особенностью дисперсного состава про­дуктов разложения КН в объеме является присутствие во всех ис­следованных образцах как малых равноосных, практически сферических частичек, так и их агрегатов нарастающих размера и сложности формы (см. рис. 12). Естественное объяснение этого основывается на рассмотрении относительных скоростей коагуля­ции и спекания частиц. Коагуляция порождает частицы сфериче­ской формы постольку, поскольку время между столкновениями двух частиц больше, чем время, необходимое для полного слия­ния (спекания) этих частиц; если же коагуляция опережает спекание, то она будет давать не сферические частицы, а их агрегаты сложной формы.

С увеличением размера частиц при их коагуляционном росте время, необходимое для полного слияния частиц (τ _спек ) рас­тет быстрее, чем время между столкновениями (τ _коаг). Поэтому, начиная с некоторого критического размера,  определяемого ус­ловием   τ _спек = τ _коаг ,  характер коагуляции должен измениться: произойдет переход от увеличения размера сферических частиц к образованию их агрегатов.

Учет этих особенностей формирования частиц порошков в тех­нологическом аппарате открывает возможность воздействия на ка­чество порошков  путем изменения условий коагуляции аэрозоля (в частности, наложением магнитных полей, действием ультра­звука, а также изменением гидродинамической обстановки в ап­парате).

Наконец, возможны чисто химические воздействия на техноло­гический процесс, включающие введение активирующих добавок. Предлагаемая схема позволяет рассматривать влияние на процесс активирующих добавок (кислород, сероводород), которые описаны в патентной литературе,одним из двух способов:

б)           добавка ускоряет гетерогенную реакцию на частицах. (Разумеется, возможно, что происходит и то и другое). В обоих случаях должно происходить как увеличение размера частиц, так и повышение степени превращения за данное время.

Таким образом, результаты проведенного физико-химического исследования дают лучшее понимание сущности уже известных тех­нологических приемов и, позволяют наметить и новые технологиче­ские варианты.

Главным результатом работы является установление общей кар­тины процесса «химической кристаллизации» никеля при термиче­ском разложении карбонила никеля в объеме. Схема процесса вклю­чает в себя следующие влияющие друг на друга стадии: гомоген­ную диссоциацию КН до трикарбонила, активированную агрегацию субкарбонильных осколков, газокинетическую коагуляцию, направ­ленную коагуляцию ферромагнитных частиц никеля,  гетерогенное разложение карбонила на частицах никеля.

Математическая модель процесса, учитывающая перечисленные стадии, позволила удовлетворительно описать наблюдаемые осо­бенности процесса, в частности, существование периодов квази­равновесия и лавинного протекания после образования достаточ­но большого количества аэрозольных частиц,

Можно предполагать, что сходные механизм и способ описания имеют силу и для других процессов химической кристаллизации в объеме.

 

Авторы приносят глубокую благодарность Н.А.Фуксу и А.Г.Сутугину за помощь в постановке этой работы, а также  М.А. Немойтину за электронно-микроскопические съемки образцов.

 

 

 

 

 

 

 

 

Табица 1. Данные о кинетике термического разложения КН в объеме
Автор и год публикации	Поверхность реактора	Температура,°C	Давление, атм	Концентрация, %	Энергия активации, ккал/моль	Кинетическое уравнение
Гаррат и Томсон, 1934 [1]	стекло	70-100	0,04-0,08	100	12,0	(2)4)
Баун, 1935[2]	-	100-128	0,02-0,08	100 и ниже	10,2	(2)4)
Чен и Макинтош, 1962 [3]	стекло никель	35-80	0,02-0,1	100 и ниже	19,1	(2)1)4)
Дей, Басоло и Пирсон, 1963 [4]	тонкий слой никеля на стекле	47-66	1	0,04	44,7±3	(2)4)
Цылов, 1971 [5]	-	100-400	1	12)	8,32)	-
Белозерский и Сегаль, 1972 [6]	стекло	60-170	1	100 и ниже	21,63)	-
Гузен и Ванденберг, 1972 [7]	никелированное стекло	50-90	0,25	100	17,2	(2)1)4)
1)      Постулировано авторами 2)      Вычислено по экспериментальным данным оригинала 3)      Для первого порядка реакции
4)      Кинетическое уравнение (2): Vv = K1nk/ (1 + K*nc )

 

 

 

 

 

Таблица 2. Характерные условия и результаты разложения КН в потоке с измерением весовой и счетной концентрации аэрозолей никеля
Номер опыта	Потоки на реактор, л/мин			Условия в реакторе				Характеристики аэрозоля				Степень превращения КН в объеме, %
	Парогазовая смесь с КН	Горячий азот	Разбавление на выходе	Время пребывания, сек		Температура,°C	Начальная концентрация КН 10-7 г/см3	Весовая концентрация, 10-9 г/см3		Счетная концентрация, 107 част/см3	Среднее число атомов в частице, млн.
1	2	3	4	5		6	7	8		9	10	11
1	0,08	1,1	-	1,9		100	0,5	0,86		0,95	0,9	5,2
2	"	"	-	"		115	"	1,95		1,6	1,2	11,3
3	"	"	-	"		125	"	1,73		2,0	0,86	10,0
4	"	"	-	"		130	"	2,25		3,5	0,64	13,1
5	"	"	-	"		135	"	4,4		3,1	1,4	25
6	"	"	-	"		140	"	9,15		1,0	9,1	53
7	"	"	-	"		145	"	17,5		0,62	28,0	100
8	0,15	5,85	6	0,02		90	3,4	8,7		3,8	2,3	7,4
9	0,10	3,90	"	0,03		"	"	11,1		1,85	6,0	9,5
10	0,10	3,90	"	0,03		"	"	8,6		3,2	2,7	7,3
11	0,052	2,05	4	0,06		"	"	6,5		0,81	8,0	5,55
12	0,052	2,05	4	0,06		"	"	9,4		0,55	17	8,0
13	0,03	1,17	3	0,1		"	"	6,6		0,42	15,5	5,6
14	0,03	1,17	3	0,1		"	"	4,5		0,125	36	3,85
15	0,04	3,0	3	0,02		"	0,28	1,88		1,0	1,9	19,5
16	0,03	3,0	3	0,02		"	0,21	1,75		1,4	1,25	24,1
17	0,04	1,46	2	0,04		"	0,28	1,5		0,95	1,6	15,5
18	0,05	2,95	3	0,02		"	1,5	7,65		1,6	4,8	14,8
19	0,08	1,5	2	0,04		"	1,2	5,2		1,15	4,5	12,5
20	0,03	0,97	2	0,06		"	1,6	5,5		0,51	11	10
21	0,02	0,60	2	0,1		"	1,3	3,1		0,16	19	7,0
22	0,045	1,0	2	0,06		"	2,7	9,2		0,23	40	9,9
23	0,055	1,0	2	0,06		"	3,2	4,4		0,275	16	4,0
24	0,100	2,9	3	0,02		"	4,0	10,2		0,57	18	7,4
25	0,06	1,95	2	0,06		"	4,2	10,7		0,30	35	6,0
26	0,12	2,88	3	0,02		"	5,3	11,5		0,34	34	6,25
27	0,04	1,16	2	0,1		"	5,6	5,1		0,085	60	2,65
28	0,08	1,95	2	0,06		"	7,1	9,5		0,30	32	3,9
29	0,05	1,15	2	0,1		"	7,1	5,4		0,26	21	2,2
30	0,04	1,15	2	0,1		90	1,65	4,15		0,48	8,6	7,3
31	"	"	"	"		110	"	3,65		0,60	6,1	6,4
32	"	"	"	"		130	"	4,8		1,3	3,7	8,4
33	"	"	"	"		150	"	5,5		0,75	7,3	9,7
34	"	"	"	"		170	"	5,2		0,86	6,05	9,15
35	0,05	2,05	2,5	0,06		90	"	7,0		0,36	19,5	12,2
36	"	"	"	"		110	"	7,7		0,50	15	13,5
37	"	"	"	"		130	"	9,1		0,75	12	16
38	"	"	"	"		150	"	9,9		0,68	14	17,4
39	"	"	"	"		170	"	10,2		0,82	12,5	17,9
40	0,02	2,16	4,6	0,1		110	6,7*10-5	1,2*10-3		15,5	7·10-5	52
41	"	"	"	"		"	6,7·10-5	0,8·10-3		4,1	2·10-4	35
42	"	"	"	"		"	6·10-4	1,7·10-3		21	8·10-5	8
43	"	"	"	"		"	6·10-4	1,1·10-3		7,0	1,5·10-4	5,3
44	"	"	"	"		"	5,6·10-3	1,0·10-3		2,0	5·10-4	0,52
45	"	"	"	"		"	5,6·10-3	2,3·10-3		1,8	1,3·10-3	1,2
46	"	"	"	"		"	0,053	4,2·10-3		1,55	2,8·10-3	0,2
47	"	"	"	"		"	0,053	1,3·10-2		1,35	1·10-2	0,7
48	"	"	"	"		"	0,57	0,047		0,78	6,2·10-2	0,24
49	"	"	"	"		"	0,57	0,152		9,1	1,7·10-2	0,77
Номера опытов					Тип реактора				Объем камеры, см3
1-7					Тройниковый				38
8-14; 25; 27-39					Рис. 2б				1,96
15-24; 26					Рис. 2б				0,98
40-49					Рис. 2а				3,6

 

Таблица 3. Размеры частиц никеля, полученных при разложении разбавленных паров КН в лабораторных реакторах
Условия разложения			Преобладающие размеры сферических частиц, Å
Температура,°C	Концентрация КН на входе в реактор, г/см3	Время пребывания в реакторе, сек
180	2·10-7	0,06	50-100
180	2·10-7	0,2	50-100
150	5·10-8	0,06	50-100
150	2·10-7	0,06	50-100
150	5·10-6	0,06	100-200
150	5·10-5	0,06	300-500
90	5·10-6	0,06	100-200
90	5·10-6	0,2	100-200
270	1,4·10-4	1,5	150-200*)
200	1,4·10-4	1,6	50-100*)
150	1,4·10-4	1,5	50-100*)
*) По данным исследования диспергированного порошкообразного продукта,  собранного на выходе из реактора

 

 

 

Рис. 1 Общая схема установки для измерения кине­тики разложения карбонила никеля в объеме и сред­него размера образующихся аэрозольных частиц
1	- подача газа-носителя (азот или СО),
2	- подача азота,
3	- контейнер-насытитель с КН,
4	- нагреватель азота,
5	- реактор (со смесителем на входе и закалочной камерой на выходе),
6	- фильтры Петрянова,
7, 8	- неселективные "разбавители" аэрозоля,
9,10	- приборы КУСТ,
11	- ультрамикроскоп
12	- нефелометр

 

 

Рис. 2. Схемы проточных реакторов для исследования кинетики разложения КН в объеме: а) металлический реактор с радиально-щелевым смесителем и закалочной камерой: 1 - реакционный объем, 2 - вход в закалочную камеру, 3 - радиально-щелевой смеситель. б) стеклянный реактор со щелевым смесителем и закалочной камерой; в) металлический реактор с радиально-щелевым смесителем и переменным реакционным объемом.

 

Рис. 3. Кинетика термического разложения КН в объеме: Точки - эксперимент (измерения в реакторе Рис. 2. в) ), сплошные линии - расчет. Температура измерений: 1,6 - 53°C; 2, 8, 9, 10 - 70°C; 4 - 75°C; 3, 5, 7 - 84°C. Начальная концентрация КН: 1, 2, 3, 4, 5, 9 - 1,08·10-7 г/см3; 6,7 - 2,83·10-7 г/см3; 8 - 2,8·10-8  г/см3; 10 - 7,1·10-7 г/см3. Отношение молярных концентраций КН/СО: 4, 5 - 1/0,5; остальное 1/0,1.

 

Рис. 4. Температурная зависимость степени превращения
Номер Кривой	Условия измерений
	Концентрация КН на входе в реактор, г/см3	Концентрация СО, г/см3	Время пребывания в реакторе, Сек
1	1,08·10-7	1,8·10-9	1,6
2	5,0·10-8	0,9·10-9	2,0
3	4,0·10-5	1,3·10-3	5,0
4	1,5·10-7	6·10-7	0,06

 

 

 

Рис. 5. Зависимость степени превращения в объеме (при влиянии осаждения на стенках) от начальной концентрации КН при 90°C и различном времени пребывания. Сплошные линии - расчет для времени пребывания: 1 - 0,02 сек, 2 - 0,10 сек

 

 

 

Рис. 6. Изменение степени превращения в присутствии окиси углерода (CO: КН = 300:1)
Обозначение точек	Температура, °C	Концентрация КН, г/см3
	60-90	(2 - 4)·10-6
	110-150	(2 - 4)·10-6
	60-90	1,5·10-7
	110-150	1,5·10-7
Пунктир отвечает отсутствию влияния CO

 

 

 

Рис. 7. Изменение степени превращения в объеме с ростом времени пребывания в реакторе (при влиянии осаждения частиц на стенках). Точки - эксперимент, сплошная линия - расчет. Условия измерений: Температура 90°C; концентрация КН 3,4·10-7 г/см3; объем реакционной камеры 1,96 см3

 

 

 

Рис. 8. Изменение степени превращения в объеме с температурой (при влиянии осаждения частиц на стенках). Точки - эксперимент, сплошная линия - расчет. Условия измерений: концентрация КН 1,6·10-7 г/см3; Время пребывания в реакторе: 1-0,06 сек, 2-0,10 сек.

 

 

Рис. 9. Влияние температуры на счетную концентрацию и размер частиц никеля: 1 - начальная концентрация КН 2·10-8 г/см3, время реакции 0,02 сек; 2 - начальная концентрация КН 1,5·10-7 г/см3, время реакции 0,06 сек. Различные обозначения точек относятся к различным сериям измерений.

 

 

 

 

Рис. 10. Влияние введения окиси углерода в газовую фазу на размер образующихся частиц. Условия и обозначения те же, что на Рис 6.

 

 

 

Рис 11. Влияние введения окиси углерода на счетную концентрацию образующегося аэрозоля. Условия и обозначения те же, что на рис 6.

 

 

 

Рис. 12.  Электронно-микроскопические снимки аэрозольных частиц никеля: а) малые равноосные частицы (увеличение 60 000); б) нитевидные агрегаты - продукт направленной коагуляции (увеличение 30 000) в) крупные агрегаты (увеличение 10 000)

 

 

Рис. 13. Зависимость счетной концентрации частиц никеля ультрамикроскопического размера от условий: 1,2 - начальная концентрация КН 0,14 и 0,05 % об.; время пребывания соответственно 10 и 15 сек; 3,4 - температура разложения 140 и 120 °C, время пребывания 15 сек

 

 

 

ЛИТЕРАТУРА

1.      А.Р. Gаггаt,   Н. W. Тоmрsоn, J. Сhеm. Soc., 1934, 1822-1825.  

2.      C. E. H. Bawn, Тгаns. Fаrаdау Sоc., 1935, 31, 440-446.

3.      R. K. Chan, R. McIntosh, Canadian J. Chem., 1962, 40, 845-855.

4.      J. Ph. Day, R. G. Pearson, F. Basolo, J. Amer. Chem. Soc., 1968,                90, 6933-6938.

5.      Б.А.  Цылов,   Порошковая металлургия,   1971,   № 5  (101), 21-26.

6.      Н. А.  Белозерский,   Л. Д. Сегаль,   Тр.  инст.   Гипроникель, 1972, вып. 53, с. 118-127.

7.      А. J. Goosen, J. A. Van den Berg, J. South African Chem. Inst., 1972,   25; 370-380.

8.      А.Я. Кипнис,   Л.А.  Померанцева,   А.Е. Рюмшин,.   Депонирова­но  в   ОНИИЕЭХИМ,   г.  Черкассы,   1978  г.,   2149/78   Деп.

9.      А.Я. Кипнис,   Л.А.  Померанцева,   А.Е. Рюмшин,.   Депонирова­но  в   ОНИИЕЭХИМ,   г.  Черкассы,   1978  г.,   2147/78   Деп.

10.   А. Е Рюмшин, А. Я. Кипнис, П. А. Кулле,  С6. "Матема­тическое моделирование  в науке к технике",   Издательство ЛТИ им.  Ленсовета,   вып. 2, ч. 2, Л., 1974

11.  А. Е Рюмшин, А. Я. Кипнис, П. А. Кулле,  С6. "Матема­тическое моделирование  в науке к технике",   Издательство ЛТИ им.  Ленсовета,   вып. 2, ч. 4, Л., 1975

12.  А.Е.  Рюмшин,   А.Я. Кипнис,   Депонировано  в ВИНИТИ,   1979 г.

13.  Н. А. Фукс, А. Г. Сутугин,   Коллоидный журнал,  1966, 28, № 1, 131-138.

14.  А.А. Мазловский,   Коллоидный журнал,  1970, 32,  № 2, 238-244.

15.   А. А. Мазловский,  Канд.  дисс,   АН Латв.  ССР, ОХН,   Рига, 1971.

16.   И. В.  Петрянов  и др.,  Волокнистые фильтрующие материалы ФП,   "Знание",   М.,   1968.

17.   А. Г.   Сутугин,  Измерительная техника,   1971,   № 8,   79-80.

18.   Я. И. Коган,   З.А. Бурнашева,  Ж.  физ.  химии,   1960,  №12, 34,   2630-2639.

19.   Е. А. Вигдорчик ЛенНИИ Гигиены труда и профзаболеваний, Л. 1948, с. 131-177.

20.   Е. Т. Лыхина, С. С. Саркисова, ГосНИИ Гигиены труда и профзаболеваний, Тр. научной сессии (1956), Л., 1958, с. 182-186.

21.   Я. И. Коган,   Заводская лаборатория,   1958,  24, №2,   215-219.

22.   А. Я.  Кипнис, Н.Ф. Михайлова,   А. Г.  Сутугин,   Авт.  свид. СССР,   № 416079,   Кл.   В.01j   1/14,   Бюлл.  изобр.   № 7,   1974.

23.   А.Г.  Сутугин,  Н.А.  Фукс,   Ж.   прикл.  механики и  техн. физики,   1968,   № 3,   134-143.

24.   М. А. Немойтин, Тр. инст. Гипроникель, вып. 21, с. 26-31.

25.   D. Beischer, A. Winkel, Naturwissenschaften, 1937, 25, 420-423.

26.   Н. А. Фукс,   Механика аэрозолей,  Изд-во  АН СССР, М.,  1955.

27.   J. Ph. Day, F. Basolo, R. G. Pearson, J. Amer. Chem. Soc., 1968,  90,      6927-6933.

28.   А. Я.  Кипнис,  З. П. Федорова,  Кинетика и катализ,  1978, 19,   вып. 4 , с. 848-852.

29.   А. Г. Сутугин,  З. И. Котцев, Н. А. Фукс,  Коллоидный журнал, 1971,  3З,   № 4,   585-591.

30.   А.Г.   Сутугин,   ДАН СССР,   1971, 201,  № 3, 647-650.

31.   А. Г.  Сутугин,   А. А. Лушников,   Теор.  основы хим.   техноло­гии,   1975, 9, № 2, 210-218.

32.   G. Zebel, Staub, 1959, 19, 381-387.

33.   И. М. Калитович, А. Я. Кипнис, Н. Ф. Михайлова, Д. Н. Таганов, Ж.   прикл.  химии,   1974, 47,  № I,   43-48.

34.А.Я. Кипнис,  Н.Ф.  Михайлова,  Совещ.  по кинетике и меха­низму хим.  реакций в  твердом теле,   Новосибирск,   1977, ч.   I,   с. 70-73.

35.А.Я. Кипнис,   А.Е.   Рюмшин,  Депонировано  в Цветметинформации,   1978 г. ,   № 371.

36.   А.Я.  Кипнис,   Е.Ф.  Михайлова,  Л.А.  Померанцева,  Депонировано  в  ВИНИТИ,   1976 г., 32-77 Деп. 3

37.   Н.А. Фукс,  Успехи механики  аэрозолей,   ВИНИТИ,  М., 1961..

38.   S. J. W. Price, in: C. H. Bamford, C. F. H. Tipper (Editors), Comprehensive            chemical kinetics, vol. 4, lsevier, Amsterdam, 1972, p. 200-202.

39.   B. Callear, Proc. Roy. Soc. London, 1961, A265, No. 1320, 88-96.

40.   W. Groth, U. Scurath, K. Weber, Z. physik. Chem. (BRD), 1974, 93, 159-171.